Dalam matematika, segitiga Pascal adalah suatu aturan geometri pada koefisien binomial dalam sebuah segitiga. Ia dinamakan sempena Blaise Pascal dalam kebanyakan dunia barat, meskipun ahli matematika lain telah mengkajinya berabad-abad sebelum dia di India, Persia, Cina, dan Italia. Barisan segitiga Pascal umumnya dihitung dimulai dengan baris kosong, dan nomor-nomor dalam barisan ganjil biasanya diatur agar terkait dengan nomor-nomor dalam baris genap. Konstruksi sederhana pada segitiga dilakukan dengan cara berikut. Di barisan nol, hanya tulis nomor 1. Kemudian, untuk membangun unsur-unsur barisan berikutnya, tambahkan nomor di atas dan di kiri dengan nomor secara langsung di atas dan di kanan untuk menemukan nilai baru. Jika nomor di kanan atau kiri tidak ada, gantikan suatu kosong pada tempatnya. Misalnya, nomor satu di barisan pertama adalah 0 + 1 = 1, di mana nomor 1 dan 3 dalam barisan ketiga ditambahkan untuk menghasilkan nomor 4 dalam barisan keempat.
Pembinaan ini terkait dengan koefisien binomial oleh Peraturan Pascal, yang menyatakan bahwa jika
adalah koefisien binomial ke-'k dalam pengembangan binomial pada (x + y)n, di mana n! adalah faktorial n, oleh itu
untuk setiap bilangan bulat bukan negatif n dan mana-mana bilangan bulat k di antara 0 dan n.
Segitiga Pascal memiliki pengitlakan dimensi lebih tinggi. Versi tiga-dimensi disebut Piramida Pascal atau Pascal 's tetrahedron, sedangkan versi umum disebut simpleks Pascal - ini lihat piramida, tetrahedron dan simpleks.
Sumber : http://id.wikipedia.org/wiki/Segitiga_Pascal


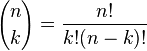

Tidak ada komentar:
Posting Komentar